Multiplicatively closed set
In abstract algebra, a subset of a ring is said to be multiplicatively closed if it is closed under multiplication (i.e., xy is in the set when x and y are in it) and contains 1 but doesn't contain 0.[1] The condition is especially important in commutative algebra, where multiplicatively closed sets are used to build localizations of commutative rings.
Contents |
Examples
Common examples of multiplicatively closed sets include:
- the set
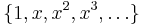 where x is not a nilpotent element;
where x is not a nilpotent element; - the set of units of the ring;
- the set of regular elements of the ring;
- in a commutative ring, the set-theoretic complement of a prime ideal.
Properties
For commutative rings, the complement of a prime ideal is an especially important example of a multiplicatively closed set. Clearly an ideal A of a commutative ring R is prime if and only if the complement R\A is multiplicatively closed. In fact, complements of prime ideals enjoy another property: that of being "saturated". A set is said to be saturated if every divisor of x in the set is also in the set (i.e., if xy is in the set, then x and y are in the set). For a commutative ring the converse is not always true: a saturated multiplicative set may not be a complement of a prime ideal. However it is true that a subset S is saturated and multiplicatively closed if and only if S is the set-theoretic complement of a non-empty set-theoretic union of prime ideals, (Kaplansky 1974, Theorem 2).
The intersection of a family of multiplicative sets is again multiplicative, and the intersection of a family of saturated sets is saturated.
Suppose S is a multiplicatively closed subset of a commutative ring R. A standard lemma due to Krull[2] states that there exists an ideal P of R maximal with respect to having empty intersection with S, and this ideal is a prime ideal. It follows that S is a subset of the complement R\P, which is a saturated multiplicatively closed set. Thus every multiplicatively closed set is a subset of a saturated multiplicatively closed set.
See also
References
- Kaplansky, Irving (1974), Commutative rings (Revised ed.), University of Chicago Press, MR0345945